Що ж таке "золотий перетин"!
У математиці та мистецтві дві величини утворюють золотий перетин , якщо співвідношення їх суми і більшої величини дорівнює співвідношенню більшої і меншої. Це відношення прийнято позначати грецькою буквою .
Золотий перетин вважається співвідношенням найвідповіднішим естетичному сприйняттю зображення, вперше запропоноване давньогрецьким математиком Евклідом. Вживається в мистецтві й архітектурі, найчастіше як золотий прямокутник. Золотий прямокутник утворюється при поділі відрізку АВ в такій точці О, що площа прямокутника, одною стороною якого є весь відрізок, а іншою — менший з відрізків, дорівнює площі квадрата з більшим відрізком як стороною
(|АВ| * |OB| = |AO|2).
Це рівняння має єдиний додатний розв'язок
Відношення двох відрізків приблизно дорівнює 13:8.
Число деколи називають золотим числом.
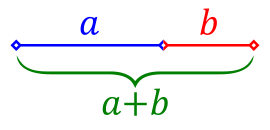
φ = (a+b) : a = a : b
У 1509 році в книжкових крамничках Венеції з’явилася невелика, витончено видана темношкіра книга. На її коричневій ворсистій обкладинці були видавлені в шаховому порядку матово-золоті слони. Любителі швидко розкупили її. Майже на кожній сторінці книги чудовою чорною фарбою були виконані гравюри, що зображували різні геометричні фігури. Чутки завзято приписували чудові гравюри руці самого Леонардо да Вінчі. На заголовному аркуші книги автор, якийсь брат Лука Пачіолі ді Бого, урочисто заявляв про зв’язки ідей книги з творами великого Платона. Книга називалася «Про Божественну пропорцію» і оповідала про одну із загадок пропорції тіл, яку поставила перед людиною природа.
Давньогрецький філософ Птолемей (II ст. до н. е.) зауважив, що висоту людської фігури можна розділити умовно на 21 відрізок. Причому більша частина – від пупа до п’ят – включала 13 відрізків, а менша – від пупа до маківки – 8. Вимірювання тіл і статуй, проведені в подальшому Леонардо да Вінчі, підтвердили цю закономірність. Висновки настільки вразили його, що він назвав співвідношення цифр 13:8 золотим перетином, а сам закон – законом золотого перетину. Під цією назвою закон і залишився в історії.
Німець Цейзинг в своїх «Естетичних дослідженнях», надрукованих у 1855 році, по суті справи, заново відкрив закон золотого перетину, про який не згадували більше двохсот років. Він показав, що цей закон проявляється не тільки в пропорціях античних статуй і добре складених людей, але й багатьох тварин, форми яких відрізняються грацією і витонченістю, і навіть комах. Найбільш докладно він розробив пропорції Аполлона Бельведерського.
Цейзинг дав суворе визначення золотому перетину і показав, як можна його отримати. Треба взяти відрізок будь-якої довжини і розділити його на дві нерівні частини так, щоб менша з них відносилась до більшої, як ця більша до всього відрізку. Але після того як цифри можливих довжин відрізків були отримані, Цейзинг з подивом виявив, що всі вони складають так званий ряд Фібоначчі: 0,1,1,2,3,5,8,13,21,34,55,89,144 .. .
Кожен легко може продовжити цей ряд до безкінечності, оскільки члени його володіють цікавою властивістю – будь-який з них дорівнює сумі двох попередніх: 0 +1 = 1; 1 + 1 = 2; 1 +2 = 3; 2 + 3 = 5; 3 + 5 = 8 і т. д.
Тепер, маючи ряд, можна було легко уточнити чисельне вираження закону, Для цього кожний наступний член ряду потрібно просто ділити на попередній: 2:1 = 2; 3:2 = 1,5; 5:3 = 1,666; 8:5 = 1 , 6; 13:8 == 1,625; 21: 13 = 1,615 …
Якщо такі відносини підраховувати далі і далі, то ми, врешті-решт, прийдемо до нескінченого десяткового дробу 1,618 …, який і є найбільш точним коефіцієнтом золотого перетину. Цей нескінчений дріб замінюють зазвичай літерою «Ф».
Цейзинг спробував прикласти шкалу золотого перетину не тільки до пропорцій живих істот, але до архітектури, археології. Він побачив «свій» закон в деяких еллінських храмах, зокрема в Парфеноні. Парфенон і закон золотого перетину! Вищий прояв прекрасного в архітектурі оцінюється рядом Фібоначчі! Цейзинг буквально приголомшений. Радісний і сподівається, що його ім’я стане поряд з іменами великих першовідкривачів законів природи – Ньютона, Гаусса, Галілея, він впевнено називає свою нову книгу: «Золотий перетин як основний морфологічний закон в природі і мистецтві».
Рамки дії закону золотого перетину з середини XIX століття почали стрімко розширюватися. Важко назвати якогось великого математика, у працях якого не залишилося б заміток щодо цього закону. Наприклад, російський математик Ю. В. Вульф прийшов до золотого перетину, вивчаючи розташування листя на стеблі рослини. Чимало мистецтвознавців виявили, як вони вважали, існування закону золотого перетину в музичних творах, тривалість окремих частин яких знаходиться в тому ж співвідношенні. Історики мистецтва сповістили світ, що в основу розрахунків пропорцій більшості споруд покладено правило золотого перетину. У цей спір внесли свою лепту навіть … кухарі. Виявилося, що відношення між великою й малою осями більшості пташиних яєць теж підкоряється великому закону.
Так закон золотого перетину незримо впровадився в нашу свідомість, увійшов у багато сторін життя. Як це не дивно, але навіть формат більшості картин, книг, аркушів паперу, листівок – не що інше, як прямокутник з відношенням сторін, що збігається з золотим перетином або близьким до нього. В кінці XIX століття навряд чи можна було зустріти хоча б одну статтю або книгу з естетики, в якій не були б сусідами поняття прекрасного і закон золотого перетину. Втім, цей великий закон «Божественної пропорції» або «золотого перетину» незримо присутній на всіх прекрасних речах, які коли-небудь були створені в минулому, і тих, які коли-небудь будуть створені в майбутньому.
Автор: Повійленко Рюрик







Немає коментарів:
Дописати коментар