Трапеція та її властивості

1. Трапеція та її властивості

Трапецією називається чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.

     Паралельні сторони трапеції називають основами, а непаралельні сторони – бічними.

    Наприклад: ABCD – трапеція, оскільки , АВ∦CD, сторони BC і AD – основи трапеції, АВ і СD – бічні сторони трапеції.

     Висотою трапеції називають перпендикуляр, проведений із будь-якої точки однієї з основ на пряму, що містить другу основу (або відстань між основами трапеції).

    Наприклад: MN – висота трапеції ABCD.

     Середньою лінією трапеції називають відрізок, що сполучає середини бічних сторін трапеції.

    Наприклад: KL – середня лінія.

     Властивості трапеції

1. Сума кутів трапеції, прилеглих до бічної сторони, дорівнює 180°.
   Наприклад: .
2. Середня лінія трапеції паралельна основам і дорівнює їх півсумі. Наприклад: .

     Трапецію, у якої бічні сторони рівні, називають рівнобічною (рівнобедреною) трапецією.

    Наприклад: ABCD – рівнобічна трапеція.

     Властивості рівнобічної трапеції

У рівнобічній трапеції:

1. Кути при основі рівні: .
2. Діагоналі рівні: AC=BD.

     Прямокутною називають трапецію, у якої одна з бічних сторін перпендикулярна до основ. Ця бічна сторона є висотою трапеції.

     Якщо у рівнобічній трапеції діагоналі взаємно перпендикулярні, то її висота дорівнює середній лінії:

.

     Коло можна описати лише навколо рівнобічної трапеції.

     Висота рівнобічної трапеції, у яку можна вписати коло, є середнім геометричним між її основами:

.

     Якщо у рівнобічну трапецію вписано коло, то її бічна сторона дорівнює середній лінії:

.

2. Формули площі трапеції 

1) Площа трапеції рівна добутку півсуми основ на висоту:

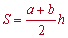
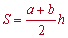
Середня лінія трапеції рівна півсумі основ, тому попередню формулу площі можна записати у вигляді

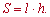
Нижче на рисунку наведено відповідні формули та позначення

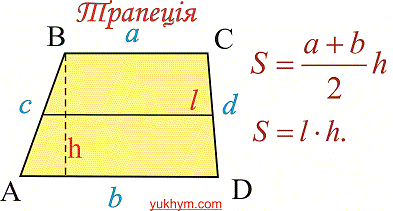
2) Якщо задано діагоналі трапеції та кут між ними (див. рис.),

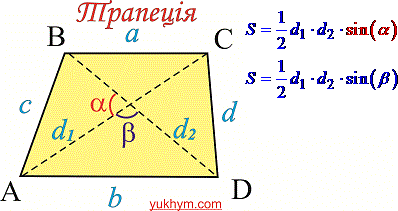
то площу трапеції знаходять за формулою

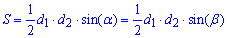
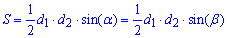
Дана формула, як і попередня, достатньо проста в обчисленнях.

Наступна формула вимагає більшої кількості розрахунків.

3) Бувають складні приклади на трапецію, коли задано усі чотири її сторони. В таких випадках використовують першу формулу площі трапеції

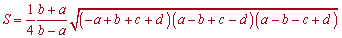
або другу

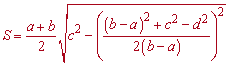
При застосуванні формули слід пам'ятати, що між сторонами повинні виконуватися умови b>a і c>d.

4) Якщо в завданні відомо, що трапеція рівнобічна (бічні сторони рівні) то для того, щоб знайти площу трапеції крім вище наведених формул використовують наступні:

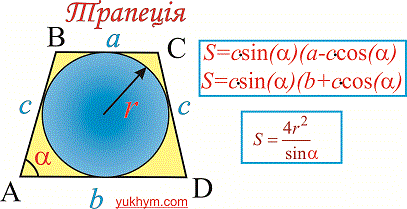
• якщо задано основу, бічну сторону та кут між ними
  
  
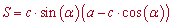
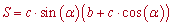
• якщо відомий радіус вписаного кола та кут при основі
  

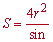
Тут r – радіус вписанного кола, alpha – кут при основі, c – бічна сторона рівнобічної трапеції.

Якщо радіуса вписаного кола та потрібного кута не задано в умові прикладу – користуйтеся вище наведеними формулами площі трапеції.

Тепер Ви знаєте як знайти площу трапеції, використовуйте наведені формули на практиці та не майте проблем у навчанні.